An Alternate to the Unified Distribution with Application to Breast Cancer Data

ABSTRACT

The Unified (θ) distribution appeared in [1], and in this short note we introduce a variant of this distribution. Further, a member of this family is shown to be significant in cancer modeling.

KEYWORDS

Bates distribution; Unified distribution; Cancer modeling

THE UNIFIED (θ) DISTRIBUTION

For x ∊(0,1) , the PDF is given by

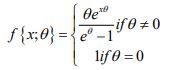
Remark 3.1. For details on the derivation of this family, see [1]

THE NEW FAMILY

Let X be Bates on (0, 1) [2], and denote its PDF as f x (x,n) and consider

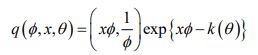
where k and ø are defined as in [1]. Suppose Q=q, and consider =a+(b-a)J, where the random variable J has density q then

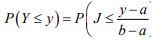
So, the CDF of Y is

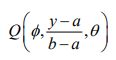
By differentiation the PDF of Y is

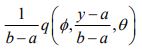
So, if ø=1, then our density becomes

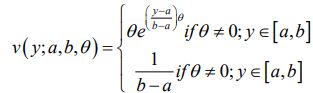
The class of all distributions with the above density is denoted A Unified (a, b, θ)

Remark 4.1. The families A Unified (a, b, θ) and Unified (θ) (of Section 1) coincide if and only if a=0 and b=1

THE UNIFIED (θ) GENERATED FAMILY OF DISTRIBUTIONS

The A Unified(a, b, θ) generated family of distributions has CDF

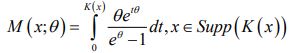
where 0 ≠θ ϵR, and K(x) is the CDF of some baseline distribution. Assuming the baseline distribution is Weibull with the following CDF

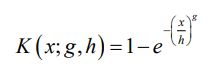
for x, g, h>0, then from the integral we have the following

Proposition 5.1. The CDF of the A Unified (0, 1, θ) Weibull family is given by

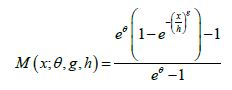
where x, g, h>0 and 0 ≠ ϵR
Obviously, the PDF can be obtained by differentiation. We write H AUW g h  (θ, , ), if H is a A Unified (a, b, θ) Weibull random variable. The family in the above Proposition is a good fit to real life data as shown below. The MLE estimates are obtained using the software MATHEMATICA (Figure 1) [3].

CONCLUDING REMARKS

In the present paper we introduced an alternate to the Unified distribution appearing in [1], and showed the Unified distribution is good in fitting real life data.

ACKNOWLEDGE

I am grateful to Oscar Alberto Quijano Acura of Concordia University, Montreal, Canada for pointing out an error in an earlier version of this paper.

REFERENCES

1. Oscar AQA (2019) The unified distribution. Journal of Statistical Distributions and Applications 6: 13.
2. Bates distribution. Wikipedia, The Free Encyclopedia.
3. Jayakumar K, Girish BM (2017) T-Transmuted X family of distributions. STATISTICA 77(3): 251-276.